アクションゲームを作るには、モノの動きをプログラムで作らなければいけません。

例えば、毎フレームに弾のX座標に２を足すと、その弾が横に動いているように見えます。プログラムの中には、大体こんな感じになります。

function update()
    bullet.pos_x = bullet.pos_x + 2 // 横動き
end

同じ様に、Y座標を変更すれば、縦に動いているように見えます。XとY座標を同時に変更すれば、斜めに動いている様に見えます。

こういう動きには加速がないので、あまり役に立たないと思います。加速を入れるには、「速度」という変数を追加します。そして、毎フレームに 速度を変えてから、位置を変更します。プログラムはこんな感じです。

function update()
    bullet.vel_x = bullet.vel_x + 0.5
    bullet.pos_x = bullet.pos_x + bullet.vel_x
end

簡単でしょう？

こういう書き方でどんな動きでもできますが、直線以外の動きはだんだん難しくなります。例えば、「巫女学校物語～沙苗編」の メニューのボタンはこういうプログラムで動きます。

function update()
    button.animation_t = button.animation_t + 1
    button.pos_x = (math.sin(button.animation_t * math.pi / 15) ^ 0.6) * 40
end

中の式はだいたいこんな感じに見えています。

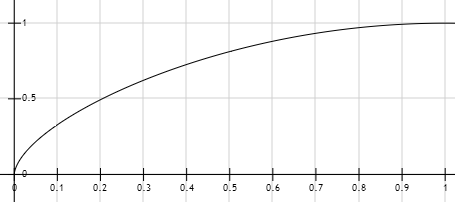
横を時間にすると、縦は位置になります。つまり、最初はボタンは速く動いて、どんどん遅くなります。是非 ミコガクを起動して、確認してみてください。

こういう風に式を書くとどんな動きでも定義できますが、調整するのはなかなか大変です。

「巫女学校～２年生」には、これより更に複雑な動きを入れたいと思いますので、ちょっと違う方法で動きを定義したいと思います。

これでベジェ曲線を紹介したいと 思います。

ベジェ曲線は非常に簡単に定義できます。

　　たくさんの複雑な動きを入れています。しかし、すべての動きに対して式を考えてプログラムに 埋め込みません。

ミコガク２で全ての動きはベジェ曲線で定義します。制御点を B0, B1, ..., BN-1 とすると、ベジェ曲線は

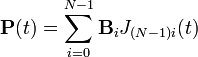
そして、

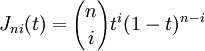
プログラムで実装するのは非常に簡単です。まずはそれそれのJを計算します(下の式)。

function calculate_polynomials(order, count)
    local polynomials = {}
    for step = 0, count do
        polynomials[step] = {}
        local t = step / count
        for i = 0, order do
            polynomials[step][i] =
                binomial_coefficient(order, i) * (t ^ i) * ((1 - t) ^ (order - i))
        end
    end
    return polynomials
end

そして、曲線を計算します(上の式)。

function calculate_point_2d(control_points, polynomials, step, order, start_point)
    local point = {}
    point.x = 0
    point.y = 0
    for k = 0, order do
        local index = start_point + k
        if control_points[index] then
            point.x = point.x + polynomials[step][k] *
                control_points[index].x
            point.y = point.y + polynomials[step][k] *
                control_points[index].y
        end
    end
    return point
end

function get_curve_2d(control_points, order, count)
    local points = {}
    points[1] = control_points[1]
    current_point = 2
    point_count = #control_points
    local polynomials = calculate_polynomials(order, count)
    for k = 1, point_count - order, order do
        for step = 1, count do
            points[current_point] =
                calculate_point_2d(control_points, polynomials, step, order, k)
            current_point = current_point + 1
        end
    end
    return points
endd

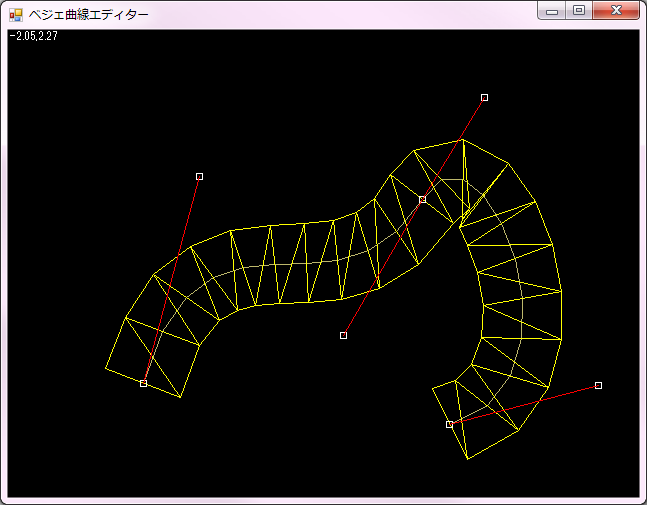
そして、曲線を簡単に編集できるエディターを作ると…

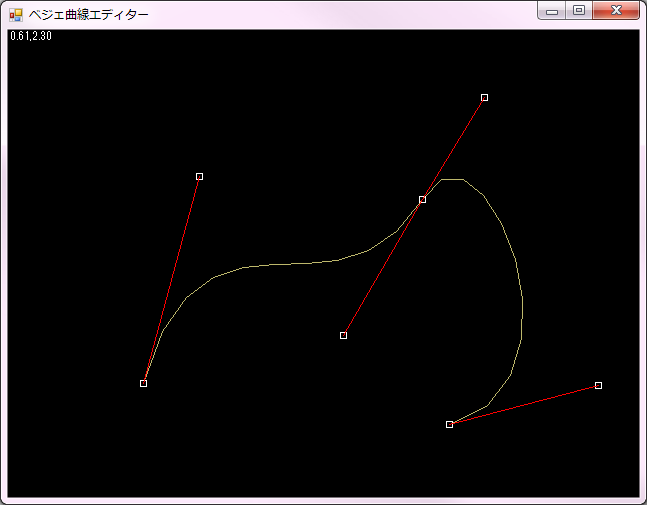
ゲーム内の全ての動きをこういう曲線で定義することができます。詳細はまたの機会にお話します。

ちなみに、ベジェ曲線を使って、メッシュを作るのも簡単です♪